Das Sortieren ist eine der am häufigsten verwendeten Funktionen beim Programmieren. Und es wird einige Zeit dauern, bis die Sortierung abgeschlossen ist, wenn wir nicht den richtigen Algorithmus verwendet haben.
In diesem Artikel werden wir verschiedene Sortieralgorithmen diskutieren.
Wir führen Sie bei jedem Schritt der Implementierung durch die verschiedenen Sortieralgorithmen. Der Implementierungsteil wird in Python sein. Sie können es einfach in jede Sprache konvertieren, sobald Sie den Algorithmus erhalten haben. Das ist die Frage der Sprachsyntax.
Wir werden in diesem Tutorial verschiedene Algorithmen vom schlechtesten bis zum besten sehen. Also keine Sorge. Folgen Sie dem Artikel und implementieren Sie sie.
Lassen Sie uns in die Sortieralgorithmen eintauchen.
Inhaltsverzeichnis
Sortieren durch Einfügen
Insertion Sort ist einer der einfachen Sortieralgorithmen. Es ist einfach zu implementieren. Und es kostet Sie mehr Zeit, ein Array zu sortieren. Es wird in den meisten Fällen nicht zum Sortieren größerer Arrays verwendet.
Der Insertion-Sort-Algorithmus behält sortierte und unsortierte Unterteile im gegebenen Array bei.
Der sortierte Teil enthält zu Beginn des Sortiervorgangs nur das erste Element. Wir nehmen ein Element aus dem unsortierten Array und platzieren es an der richtigen Position im sortierten Sub-Array.
Sehen wir uns Schritt für Schritt die visuellen Illustrationen der Einfügungssortierung anhand eines Beispiels an.
Sehen wir uns die Schritte zum Implementieren der Einfügesortierung an.
- Initialisieren Sie das Array mit Dummy-Daten (Ganzzahlen).
- Iterieren Sie vom zweiten Element über das angegebene Array.
- Nehmen Sie die aktuelle Position und das Element in zwei Variablen.
- Schreiben Sie eine Schleife, die iteriert, bis das erste Element des Arrays oder das Element auftritt, das kleiner als das aktuelle Element ist.
- Aktualisieren Sie das aktuelle Element mit dem vorherigen Element.
- Dekrement der aktuellen Position.
- Hier muss die Schleife entweder den Anfang des Arrays erreichen oder ein kleineres Element als das aktuelle Element finden. Ersetzen Sie das aktuelle Positionselement durch das aktuelle Element.
Die Zeitkomplexität der Einfügesortierung ist O(n^2) und die Raumkomplexität ist O(1).
Das ist es; Wir haben das angegebene Array sortiert. Lassen Sie uns den folgenden Code ausführen. Ich hoffe, Sie haben Python installiert, wenn nicht, sehen Sie sich die Installationsanleitung an. Alternativ können Sie einen Online-Python-Compiler verwenden.
def insertion_sort(arr, n): for i in range(1, n): ## current position and element current_position = i current_element = arr[i] ## iteratin until ### it reaches the first element or ### the current element is smaller than the previous element while current_position > 0 and current_element < arr[current_position - 1]: ## updating the current element with previous element arr[current_position] = arr[current_position - 1] ## moving to the previous position current_position -= 1 ## updating the current position element arr[current_position] = current_element if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] insertion_sort(arr, 9) ## printing the array print(str(arr))
Auswahl sortieren
Die Auswahlsortierung ähnelt der Einfügungssortierung mit einem kleinen Unterschied. Dieser Algorithmus unterteilt das Array auch in sortierte und unsortierte Unterteile. Und dann nehmen wir bei jeder Iteration das kleinste Element aus dem unsortierten Unterteil und platzieren es an der letzten Position des sortierten Unterteils.
Lassen Sie uns zum besseren Verständnis Abbildungen der Auswahl sortieren.
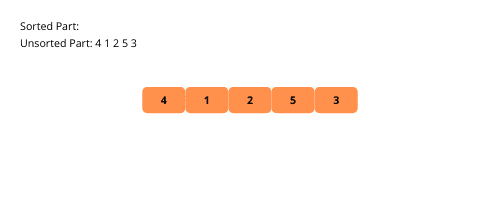
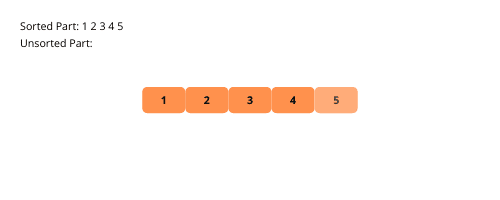
Sehen wir uns die Schritte zum Implementieren der Auswahlsortierung an.
- Initialisieren Sie das Array mit Dummy-Daten (Ganzzahlen).
- Iteriere über das angegebene Array.
- Behalten Sie den Index des minimalen Elements bei.
- Schreiben Sie eine Schleife, die vom aktuellen Element zum letzten Element iteriert.
- Überprüfen Sie, ob das aktuelle Element kleiner als das minimale Element ist oder nicht.
- Wenn das aktuelle Element kleiner als das minimale Element ist, dann ersetzen Sie den Index.
- Wir haben den minimalen Elementindex bei uns. Tauschen Sie das aktuelle Element mithilfe der Indizes gegen das minimale Element aus.
Die Zeitkomplexität der Auswahlsortierung ist O(n^2) und die Raumkomplexität ist O(1).
Versuchen Sie, den Algorithmus zu implementieren, da er dem Insertion Sort ähnelt. Sie können den Code unten sehen.
def selection_sort(arr, n): for i in range(n): ## to store the index of the minimum element min_element_index = i for j in range(i + 1, n): ## checking and replacing the minimum element index if arr[j] < arr[min_element_index]: min_element_index = j ## swaping the current element with minimum element arr[i], arr[min_element_index] = arr[min_element_index], arr[i] if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] selection_sort(arr, 9) ## printing the array print(str(arr))
Blasensortierung
Bubble Sort ist ein einfacher Algorithmus. Es tauscht die angrenzenden Elemente bei jeder Iteration wiederholt aus, bis das angegebene Array sortiert ist.
Es iteriert über das Array und verschiebt das aktuelle Element an die nächste Position, bis es kleiner als das nächste Element ist.
Illustrationen helfen uns, die Blasensortierung visuell zu verstehen. Lass sie uns sehen.
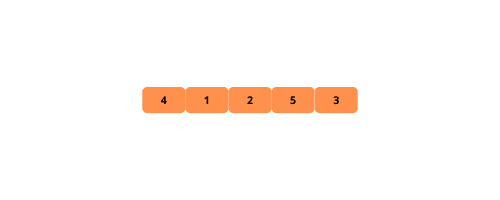
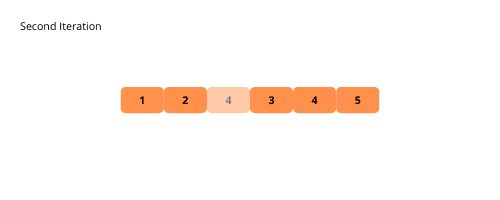
Sehen wir uns die Schritte zum Implementieren der Blasensortierung an.
Die Zeitkomplexität der Blasensortierung ist O(n^2) und die Raumkomplexität ist O(1).
Sie können die Blasensortierung inzwischen problemlos implementieren. Sehen wir uns den Code an.
def bubble_sort(arr, n): for i in range(n): ## iterating from 0 to n-i-1 as last i elements are already sorted for j in range(n - i - 1): ## checking the next element if arr[j] > arr[j + 1]: ## swapping the adjucent elements arr[j], arr[j + 1] = arr[j + 1], arr[j] if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] bubble_sort(arr, 9) ## printing the array print(str(arr))
Zusammenführen, sortieren
Mergesort ist ein rekursiver Algorithmus zum Sortieren des angegebenen Arrays. Es ist effizienter als die zuvor diskutierten Algorithmen in Bezug auf die Zeitkomplexität. Es folgt dem „Teile und herrsche“-Ansatz.
Der Merge-Sort-Algorithmus teilt das Array in zwei Hälften und sortiert sie separat. Nach dem Sortieren der beiden Hälften des Arrays werden sie zu einem einzigen sortierten Array zusammengeführt.
Da es sich um einen rekursiven Algorithmus handelt, teilt er das Array, bis das Array das am einfachsten zu sortierende (Array mit einem Element) wird.
Es ist Zeit für Illustrationen. Mal sehen.
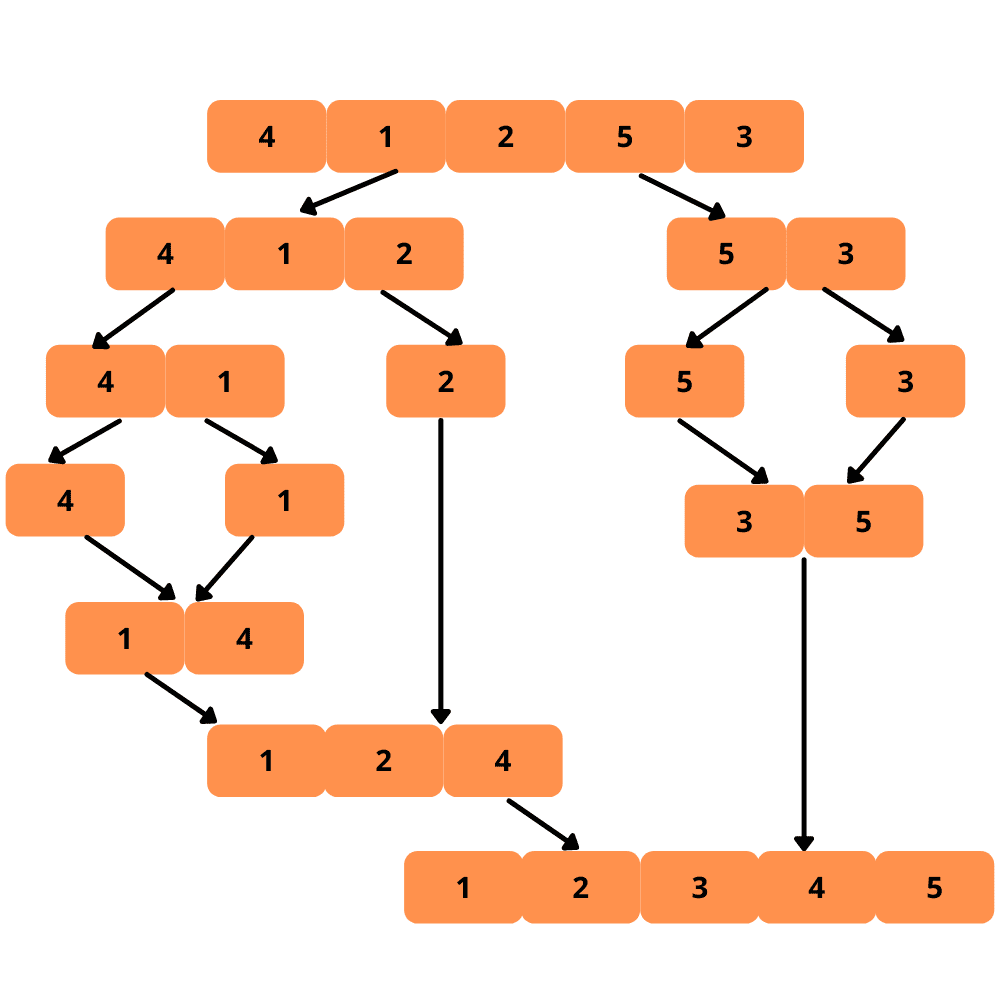
Sehen wir uns die Schritte zum Implementieren der Zusammenführungssortierung an.
- Initialisieren Sie das Array mit Dummy-Daten (Ganzzahlen).
- Schreiben Sie eine Funktion namens merge, um Unterarrays zu einem einzigen sortierten Array zusammenzuführen. Es akzeptiert die Argumente Array, linke, mittlere und rechte Indizes.
- Holen Sie sich die Längen der linken und rechten Sub-Array-Längen unter Verwendung der angegebenen Indizes.
- Kopieren Sie die Elemente aus dem Array in die jeweiligen linken und rechten Arrays.
- Iteriere über die zwei Subarrays.
- Vergleichen Sie die beiden Teilarray-Elemente.
- Ersetzen Sie das Array-Element durch das kleinere Element aus den beiden Sub-Arrays zum Sortieren.
- Überprüfen Sie, ob in beiden Teilarrays noch Elemente vorhanden sind.
- Fügen Sie sie dem Array hinzu.
- Schreiben Sie eine Funktion namens merge_sort mit Parametern Array, linkem und rechtem Index.
- Wenn der linke Index größer oder gleich dem rechten Index ist, dann zurück.
- Finden Sie den Mittelpunkt des Arrays, um das Array in zwei Hälften zu teilen.
- Rufen Sie merge_sort rekursiv auf, indem Sie die linken, rechten und mittleren Indizes verwenden.
- Führen Sie nach den rekursiven Aufrufen das Array mit der Zusammenführungsfunktion zusammen.
Die Zeitkomplexität der Zusammenführungssortierung ist O(nlogn) und die Raumkomplexität ist O(1).
Das war’s für die Implementierung des Merge-Sort-Algorithmus. Überprüfen Sie den folgenden Code.
def merge(arr, left_index, mid_index, right_index): ## left and right arrays left_array = arr[left_index:mid_index+1] right_array = arr[mid_index+1:right_index+1] ## getting the left and right array lengths left_array_length = mid_index - left_index + 1 right_array_length = right_index - mid_index ## indexes for merging two arrays i = j = 0 ## index for array elements replacement k = left_index ## iterating over the two sub-arrays while i < left_array_length and j < right_array_length: ## comapring the elements from left and right arrays if left_array[i] < right_array[j]: arr[k] = left_array[i] i += 1 else: arr[k] = right_array[j] j += 1 k += 1 ## adding remaining elements from the left and right arrays while i < left_array_length: arr[k] = left_array[i] i += 1 k += 1 while j < right_array_length: j += 1 k += 1 def merge_sort(arr, left_index, right_index): ## base case for recursive function if left_index >= right_index: return ## finding the middle index mid_index = (left_index + right_index) // 2 ## recursive calls merge_sort(arr, left_index, mid_index) merge_sort(arr, mid_index + 1, right_index) ## merging the two sub-arrays merge(arr, left_index, mid_index, right_index) if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] merge_sort(arr, 0, 8) ## printing the array print(str(arr))
Fazit
Es gibt viele andere Sortieralgorithmen, aber oben sind einige der häufig verwendeten. Ich hoffe, es hat Ihnen Spaß gemacht, das Sortieren zu lernen.
Informieren Sie sich als Nächstes über Suchalgorithmen.
Viel Spaß beim Programmieren 🙂 👨💻
