Der prozentuale Fehler in einer Datensammlung ist die Differenz zwischen den exakten und ungefähren Werten im Vergleich zum ursprünglichen Wert. Dieser prozentuale Fehler wird in Prozent ausgedrückt und somit mit 100 multipliziert.
Sie können den prozentualen Fehler als absoluten oder relativen Fehler ausdrücken. Fehler können aufgrund von Präzisionsfehlern in einer Maschine, Rechenfehlern, Messfehlern oder Umgebungsbedingungen auftreten.
Prozentuale Fehler helfen uns zu bestimmen, wie signifikant unsere Fehler während einer Analyse sind. Kleinere prozentuale Fehler bedeuten, dass wir uns dem ursprünglichen Wert nähern, größere prozentuale Fehler bedeuten eine erhebliche Abweichung zwischen dem tatsächlichen Wert und dem ungefähren Wert.
Ein Fehler von 2 % würde beispielsweise bedeuten, dass wir dem ursprünglichen Wert sehr nahe kommen, während ein Fehler von 56 % einen massiven Unterschied zwischen dem tatsächlichen und dem ungefähren Wert bedeuten würde.
Fehler beim Messen sind allgegenwärtig, da Hände während des Messens zittern können, Instrumente fehlerhaft sein können, Material möglicherweise nicht präzise ist usw.
Inhaltsverzeichnis
Berechnung des prozentualen Fehlers
Um den prozentualen Fehler zu berechnen, müssen Sie zwei verfügbare Werte haben. Einer ist der genaue Wert und der zweite ist der ungefähre Wert. Subtrahiere diese beiden Werte und dividiere sie dann durch den ursprünglichen Wert. Da der prozentuale Fehler in Form von Prozent ausgedrückt wird, multiplizieren Sie die so erhaltene Zahl mit 100. Mit anderen Worten, der prozentuale Fehler ist der relative Fehler multipliziert mit 100.
Prozentsatz Fehler = [(Actual Value – Expected Value) / Expected Value] × 100
Bestandteile der Formel
Istwert: Der Istwert gibt den numerischen Wert eines bestimmten Messwerts an. Der tatsächliche Wert hätte beim Ablesen erfasst werden sollen, aber aufgrund einiger Fehler konnten wir diesen Wert nicht erfassen. Es ist ein gängiger Wert, der sich ideal zum Durchführen von Berechnungen eignet.
Erwartungswert: Der Erwartungswert gibt den beim Experimentieren aufgezeichneten Messwert an. Aufgrund von Fehlern entspricht er in den meisten Fällen nicht dem tatsächlichen Wert. Fehler können auf Fehler in der Maschine, Fehler bei der Messung oder Umgebungsfaktoren wie Luft oder zerbrochene und beschädigte Instrumente zurückzuführen sein.
Einige Beispiele
Beispiel 1
Ein Junge maß die Fläche eines Dreiecks, und laut ihm betrug der Messwert 462 cm². Die ursprüngliche Fläche des Quadrats beträgt jedoch 465 cm². Berechnen Sie den prozentualen Fehler.
Lösung
Wert der gemessenen Fläche = 462 cm²
Wert der tatsächlichen Fläche = 465 cm²
Berechnung
Differenz Istwert – Messwert: 465-462 = 3
3 ist also der Messfehler.
Teilen Sie den Fehler durch den tatsächlichen Wert – 3/465 = 0,00645
Multiplizieren des erhaltenen Wertes mit 100 – 0,00645 x 100 = 0,64 %.
Daher beträgt der prozentuale Fehler bei der Berechnung der Fläche eines Dreiecks 0,64 %.
Beispiel 2
Angenommen, Sie planen eine Party und schätzungsweise 20 Personen würden an der Party teilnehmen, während nur 18 Personen kommen konnten. Berechnen Sie den prozentualen Fehler in Ihrer Schätzung.
Lösung
Die ursprünglich erwartete Anzahl von Personen = 20
Leute, die gekommen sind = 18
Berechnung
Differenz Istwert – Endwert = 20 – 18 = 2
Also, 2 ist der Fehler hier drüben.
Teilen Sie den Fehler durch den tatsächlichen Wert – 2/20 = 0,1
Wert mit 100 multiplizieren – 0,1 x 100 = 10 %
Daher beträgt der prozentuale Fehler bei der Schätzung der Gästezahl 10 %.
Beispiel 3
Angenommen, Sie haben ein Experiment durchgeführt, um den Siedepunkt von Wasser zu messen, und während des Experiments haben Sie 102 °C als Ergebnis gefunden. Der tatsächliche Gefrierpunkt von Wasser liegt bei 100°C.
Lösung
Der tatsächliche Siedepunkt von Wasser = 100° C
Der aufgezeichnete Siedepunkt von Wasser = 102°C
Berechnung
Die Differenz zwischen dem tatsächlichen Wert und dem berechneten Wert = 100 -102 = 2 °C (Prozentfehler kann niemals negativ sein, also behalten wir ihn nur positiv).
Also, 2 ist der Fehler hier drüben.
Teilen Sie den Fehler durch den tatsächlichen Wert – 2/100 = 0,02
Multiplizieren des erhaltenen Wertes mit 100 – 0,02 x 100 = 2 %
Daher beträgt der prozentuale Fehler bei der Messung des Siedepunkts von Wasser 2 %.
Szenarien aus der realen Welt, in denen der prozentuale Fehler wichtig ist
- Der prozentuale Fehler spielt eine wichtige Rolle bei der Feststellung, ob eine bestimmte Aufgabe, die Sie erledigt haben, den Anforderungen entspricht oder nicht. Es hilft Ihnen, Ihre Fehler aufzuzeigen.
- Der prozentuale Fehler kann bei Laborverfahren und großen Industrien hilfreich sein, in denen kein Spielraum für den kleinsten Fehler besteht.
- Der prozentuale Fehler wird auch verwendet, wenn wir eine Großbestellung abschließen müssen und es bei der Fertigstellung keinen Fehlerbereich geben kann.
- In wissenschaftlichen Labors ist die Verwendung des prozentualen Fehlers kritisch.
Prozentfehler vs. absoluter Fehler
Ein absoluter Fehler bei einer Messung ist die Differenz zwischen dem tatsächlichen und dem berechneten Wert. Die Einheit des Grundfehlers ist die gleiche wie der Anfangswert.
Beispiel
Angenommen, Sie wollten 2 kg Mangos kaufen, während der Ladenbesitzer 1,98 kg für Sie gemessen hat. Der absolute Fehler beträgt in diesem Fall 2 – 1,98 = 0,02.
Andererseits wird der prozentuale Fehler berechnet, indem der absolute Fehler durch den ursprünglichen Wert dividiert und dann das erhaltene Ergebnis mit 100 multipliziert wird. Der prozentuale Fehler ist eine einheitslose Größe.
Im obigen Beispiel beträgt der absolute Fehler 0,02.
Um nun den prozentualen Fehler zu berechnen, teilen wir ihn durch 20.
0,02/20 = 0,001
Der prozentuale Fehler beträgt in diesem Fall also 0,001 x 100 = 0,1 %.
Prozentfehler vs. relativer Fehler
Der relative Fehler in jeder Berechnung ist der absolute Fehler dividiert durch den tatsächlichen Wert. Das bedeutet, dass der prozentuale Fehler die Differenz zwischen dem wahren Wert und dem beobachteten Wert dividiert durch den tatsächlichen Wert ist.
Beispiel
Der Wetterbericht hat für heute 38°C erwartet. Es stieg jedoch auf 42°C.
Zuerst finden wir die Differenz zwischen den beiden Zahlen, dh dem erwarteten Wert und dem tatsächlichen Wert.
42° – 38° = 4°C
Um nun den relativen Fehler zu berechnen, teilen wir diese Zahl durch die tatsächliche Zahl, dh 38 °C
4/38 = 0,1052
Andererseits ist der prozentuale Fehler ein relativer Fehler multipliziert mit 100.
Im obigen Beispiel beträgt der prozentuale Fehler 0,1052 x 100 = 10,52 %.
Jetzt finden Sie es vielleicht ziemlich einfach, den prozentualen Fehler, den relativen Fehler oder den absoluten Fehler zu berechnen.
Sie können die Berechnung des prozentualen Fehlers vereinfachen, indem Sie die Hilfe mehrerer Online-Rechner für den prozentualen Fehler in Anspruch nehmen. Jetzt müssen Sie sich nicht mehr fragen, wie Sie den prozentualen Fehler berechnen, denn diese Rechner können das alles für Sie erledigen.
Tools zur Fehlerberechnung
#1. Rechnersuppe
Das Rechnersuppe hilft Ihnen, den prozentualen Fehler zwischen dem experimentellen Wert und dem tatsächlichen Wert zu berechnen. Sie müssen lediglich die Werte eingeben und auf die Ergebnisse warten. Der Rechner führt alle Berechnungen selbst durch und liefert Ihnen genaue Ergebnisse.
Die Seite zeigt zwei verschiedene Spalten an, in denen Sie den Wert der Zahlen eingeben, für die Sie den prozentualen Fehler berechnen möchten, und den Taschenrechner den Rest der Magie erledigen lassen.
#2. Rechner.net
Rechner.net hat zwei Spalten, in denen Sie die tatsächlichen und geschätzten Werte eingeben und den Rechner den Rest der Berechnungen erledigen lassen. Dies ist praktisch, wenn Sie viele Datenbeispiele berechnen möchten und Sie nicht die Zeit haben, den prozentualen Fehler in jedem Fall manuell zu berechnen. Der Rechner erleichtert den Vorgang und gibt Ihnen ohne große Verzögerung sofort die Antwort.

Prozentfehler sind unvermeidlich. Sie können ihren Wert nur verringern, aber es tritt kein Vorfall auf, wenn der Messwert des prozentualen Fehlers auf Null geht. Es kann ungefähr null sein, aber niemals genau null.
#3. Gute Rechner
Viele Online-Rechner können Ihnen bei der Lösung Ihrer prozentualen Fehlerprobleme helfen. Eines der praktischsten davon ist das Gute Rechner. In diesen Rechner geben Sie einfach den geschätzten und den ursprünglichen Wert ein, und die Ergebnisse werden automatisch angezeigt.
Es erspart Ihnen den Aufwand umfangreicher Berechnungen und schont Ihre Zeit. Sie können umfangreiche Berechnungen innerhalb von Sekunden schnell lösen und sparen viel Zeit.
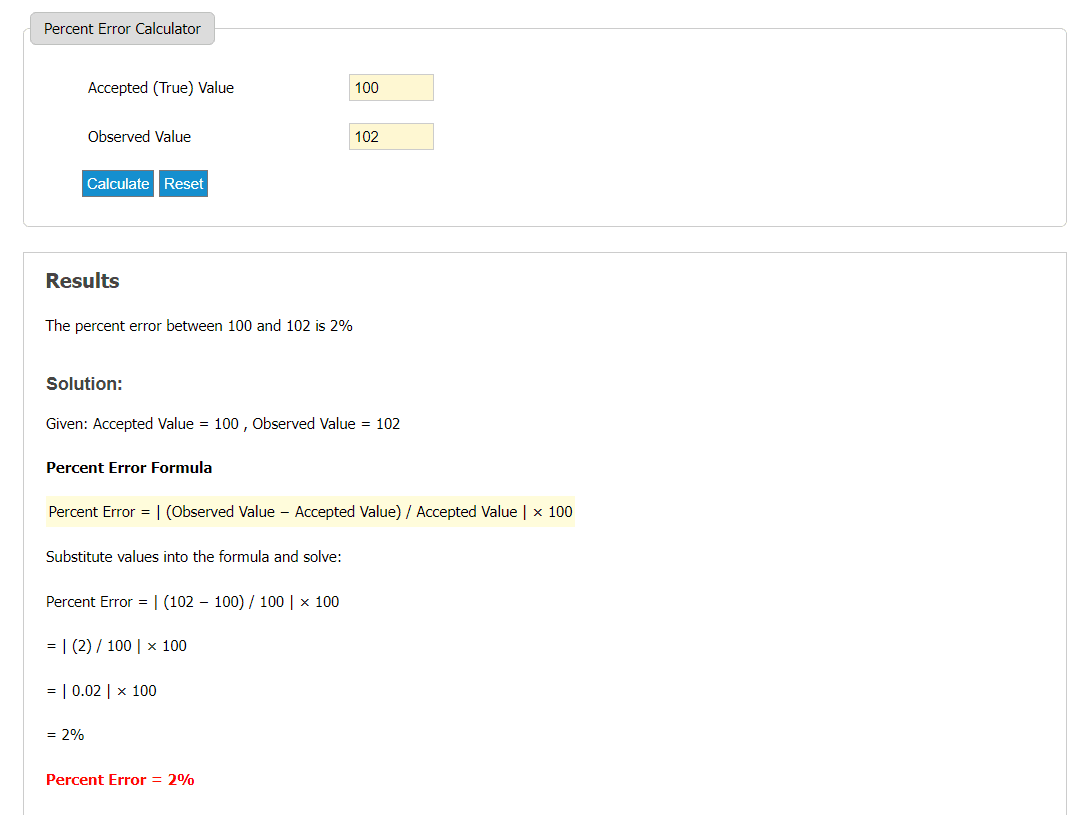
Daher ist ein Taschenrechner ideal für die Berechnung des prozentualen Fehlers, wenn Sie umfangreiche Daten zur Verfügung haben, aber die Zeit knapp wird.
Fazit
Fehler in Berechnungen können jedes Projekt oder jede Forschung komplett ruinieren. Hier können Sie die Hilfe von Online-Prozentfehlerrechnern in Anspruch nehmen, um die Arbeit effizienter und ohne menschliche Fehler zu erledigen.
Wenn Sie sich mit Finanzen beschäftigen, können Sie sich einige dieser Gewinnprozentsatzrechner ansehen.

