Entdecken Sie alles Wissenswerte über die explorative Datenanalyse, einen entscheidenden Prozess zur Aufdeckung von Trends und Mustern. Dabei werden Datensätze mit statistischen Zusammenfassungen und grafischen Darstellungen analysiert und zusammengefasst.
Wie jedes anspruchsvolle Projekt ist auch ein Data-Science-Projekt ein umfangreicher Prozess, der Zeit, eine gute Strukturierung und die gewissenhafte Einhaltung verschiedener Schritte erfordert. Die explorative Datenanalyse (EDA) stellt hierbei einen der Kernschritte dar.
In diesem Artikel werden wir uns daher kurz mit der Frage beschäftigen, was die explorative Datenanalyse eigentlich ist und wie man sie mit der Programmiersprache R durchführen kann!
Was verbirgt sich hinter der explorativen Datenanalyse?
Die explorative Datenanalyse dient der Untersuchung und Analyse der Merkmale eines Datensatzes, bevor dieser in einer Anwendung verwendet wird – sei es in der Wirtschaft, der Statistik oder im Bereich des maschinellen Lernens.

Diese Zusammenfassung der Art der Informationen und ihrer wesentlichen Merkmale erfolgt üblicherweise durch visuelle Methoden, wie beispielsweise grafische Darstellungen und Tabellen. Die praktische Anwendung geschieht im Voraus, um das Potenzial dieser Daten abzuschätzen, die in der Folge einer komplexeren Bearbeitung unterzogen werden.
Die EDA ermöglicht daher:
- Hypothesen für die Verwendung dieser Informationen zu formulieren;
- Verborgene Details in der Datenstruktur aufzudecken;
- Fehlende Werte, Ausreißer oder ungewöhnliches Verhalten zu identifizieren;
- Trends und relevante Variablen im Gesamten zu entdecken;
- Irrelevante oder mit anderen korrelierende Variablen zu verwerfen;
- Die zu verwendende formale Modellierung festzulegen.
Wo liegt der Unterschied zwischen deskriptiver und explorativer Datenanalyse?
Es gibt zwei Hauptarten der Datenanalyse: die deskriptive und die explorative Analyse. Trotz unterschiedlicher Ziele arbeiten sie Hand in Hand.
Während sich die deskriptive Analyse auf die Beschreibung des Verhaltens von Variablen konzentriert, beispielsweise durch Mittelwert, Median, Modus usw.,
zielt die explorative Analyse darauf ab, Beziehungen zwischen Variablen zu erkennen, vorläufige Erkenntnisse zu gewinnen und die Modellierung auf die gängigen Paradigmen des maschinellen Lernens auszurichten: Klassifizierung, Regression und Clustering.
Obwohl sich beide Methoden der grafischen Darstellung bedienen können, ist es allein die explorative Analyse, die versucht, umsetzbare Erkenntnisse zu gewinnen, also solche, die Entscheidungsträger zum Handeln bewegen.
Während die explorative Datenanalyse versucht, Probleme zu lösen und Lösungsansätze zu entwickeln, die als Leitfaden für die Modellierungsschritte dienen, hat die deskriptive Analyse – wie der Name schon sagt – lediglich das Ziel, eine detaillierte Beschreibung des jeweiligen Datensatzes zu liefern.
| Deskriptive Analyse | Explorative Datenanalyse |
| Analysiert das Verhalten | Analysiert Verhalten und Beziehungen |
| Liefert eine Zusammenfassung | Führt zu Spezifikationen und Maßnahmen |
| Organisiert Daten in Tabellen und Diagrammen | Organisiert Daten in Tabellen und Diagrammen |
| Hat keine nennenswerte Aussagekraft | Hat eine nennenswerte Aussagekraft |
Einige praxisnahe Anwendungsfälle der EDA
#1. Digitales Marketing
Das digitale Marketing hat sich von einem kreativen Prozess zu einem datengetriebenen Ansatz entwickelt. Marketingorganisationen nutzen explorative Datenanalysen, um die Ergebnisse von Kampagnen oder Maßnahmen zu ermitteln sowie um Verbraucherinvestitionen und Entscheidungen hinsichtlich des Targetings zu lenken.
Demografische Studien, Kundensegmentierung und andere Techniken ermöglichen es Marketingexperten, große Mengen an Kauf-, Umfrage- und Paneldaten von Verbrauchern zu nutzen, um strategisches Marketing zu verstehen und zu kommunizieren.
Die Web Exploratory Analytics ermöglicht es Marketern, Informationen auf Sitzungsebene über Interaktionen auf einer Website zu sammeln. Google Analytics ist ein Beispiel für ein kostenloses und weitverbreitetes Analysetool, das Marketer zu diesem Zweck verwenden.
Zu den im Marketing häufig verwendeten explorativen Techniken gehören die Marketing-Mix-Modellierung, Preis- und Werbeanalysen, die Verkaufsoptimierung sowie explorative Kundenanalysen, wie beispielsweise die Segmentierung.
#2. Explorative Portfolioanalyse
Ein üblicher Anwendungsfall der explorativen Datenanalyse ist die explorative Portfolioanalyse. Eine Bank oder eine Kreditagentur hat eine Sammlung von Konten mit unterschiedlichem Wert und Risiko.
Die Konten können sich je nach sozialem Status des Inhabers (reich, Mittelklasse, arm usw.), geografischer Lage, Nettovermögen und vielen anderen Faktoren unterscheiden. Der Kreditgeber muss die Rendite des Kredits mit dem Ausfallrisiko für jeden Kredit abwägen. Dann stellt sich die Frage, wie man das Portfolio als Ganzes bewertet.
Der Kredit mit dem geringsten Risiko kann für sehr wohlhabende Personen bestimmt sein, jedoch gibt es nur eine begrenzte Anzahl von wohlhabenden Personen. Auf der anderen Seite können Kredite an eine Vielzahl einkommensschwacher Personen vergeben werden, aber mit einem höheren Risiko.
Die explorative Datenanalyselösung kann die Zeitreihenanalyse mit einer Reihe anderer Faktoren kombinieren, um zu entscheiden, wann Geld an diese verschiedenen Segmente von Kreditnehmern verliehen werden soll und zu welchem Zinssatz. Die Zinsen werden den Mitgliedern eines Portfoliosegments berechnet, um Verluste zwischen den Mitgliedern dieses Segments abzudecken.
#3. Explorative Risikoanalyse
Vorhersagemodelle im Bankwesen werden entwickelt, um Gewissheit über die Risikobewertung für einzelne Kunden zu geben. Kredit-Scores sollen das säumige Verhalten einer Person vorhersagen und werden häufig zur Beurteilung der Kreditwürdigkeit jedes Antragstellers eingesetzt.
Darüber hinaus werden Risikoanalysen in der Wissenschaft und der Versicherungsbranche durchgeführt. Sie werden auch häufig in Finanzinstituten wie Online-Payment-Gateway-Unternehmen eingesetzt, um zu analysieren, ob eine Transaktion legitim oder betrügerisch ist.
Zu diesem Zweck wird die Transaktionshistorie des Kunden herangezogen. Dies wird häufiger bei Kreditkartentransaktionen angewandt; Wenn das Transaktionsvolumen des Kunden plötzlich ansteigt, erhält der Kunde einen Bestätigungsanruf, um sicherzustellen, dass er die Transaktion initiiert hat. Dies hilft auch, Verluste aufgrund solcher Umstände zu minimieren.
Explorative Datenanalyse mit R
Um die EDA mit R durchzuführen, benötigen Sie zunächst R Base und R Studio (IDE). Anschließend müssen die folgenden Pakete installiert und geladen werden:
#Pakete installieren
install.packages("dplyr")
install.packages("ggplot2")
install.packages("magrittr")
install.packages("tsibble")
install.packages("forecast")
install.packages("skimr")
#Pakete laden
library(dplyr)
library(ggplot2)
library(magrittr)
library(tsibble)
library(forecast)
library(skimr)
Für dieses Tutorial verwenden wir einen in R integrierten Wirtschaftsdatensatz, der jährliche Wirtschaftsindikatordaten der US-Wirtschaft bereitstellt. Wir werden den Namen der Einfachheit halber in „econ“ ändern:
econ <- ggplot2::economics
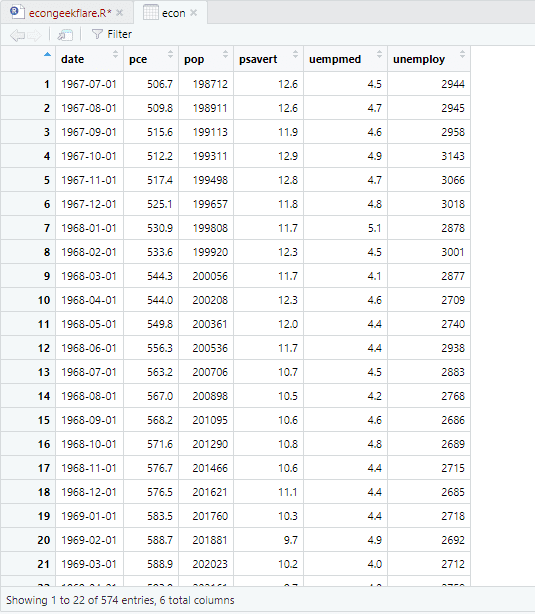
Um eine deskriptive Analyse durchzuführen, verwenden wir das Paket `skimr`, welches diese Statistiken auf übersichtliche und einfache Weise berechnet:
#Deskriptive Analyse skimr::skim(econ)

Alternativ können Sie auch die Funktion `summary` für die deskriptive Analyse verwenden:
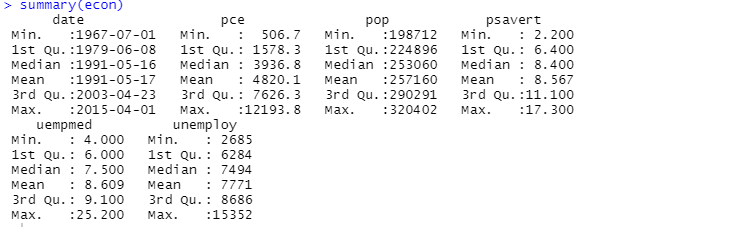
Die deskriptive Analyse zeigt, dass der Datensatz 547 Zeilen und 6 Spalten hat. Der niedrigste Wert bezieht sich auf den 1. Juli 1967 und der höchste Wert auf den 1. April 2015. Ebenso werden der Mittelwert und die Standardabweichung angegeben.
Nachdem wir nun eine grundlegende Vorstellung davon haben, was sich im „econ“-Datensatz befindet, wollen wir ein Histogramm der Variable „uempmed“ zeichnen, um die Daten genauer zu betrachten:
#Histogramm der Arbeitslosigkeit econ %>% ggplot2::ggplot() + ggplot2::aes(x = uempmed) + ggplot2::geom_histogram() + labs(x = "Arbeitslosigkeit", title = "Monatliche Arbeitslosenquote in den USA zwischen 1967 und 2015")
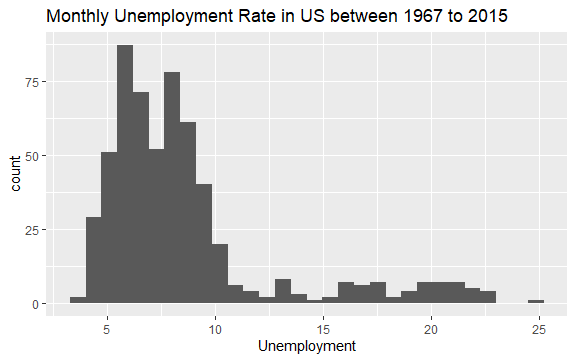
Die Verteilung des Histogramms zeigt einen länglichen Ausläufer nach rechts; das heißt, es gibt möglicherweise einige Beobachtungen dieser Variablen mit „extremeren“ Werten. Die Frage ist: In welchem Zeitraum sind diese Werte aufgetreten und wie sieht der Trend der Variablen aus?
Der einfachste Weg, den Trend einer Variablen zu erkennen, ist ein Liniendiagramm. Nachfolgend erstellen wir ein Liniendiagramm und fügen eine Glättungslinie hinzu:
#Liniendiagramm der Arbeitslosigkeit econ %>% ggplot2::autoplot(uempmed) + ggplot2::geom_smooth()
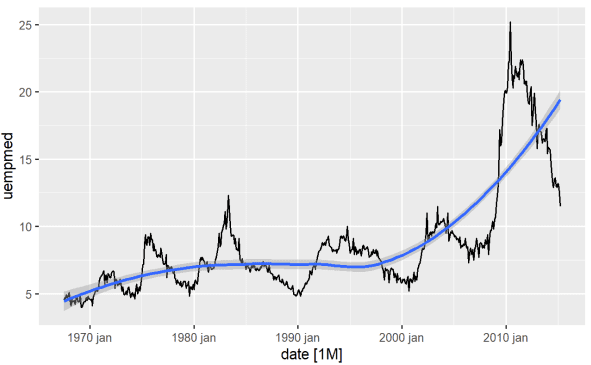
Aus dieser Grafik geht hervor, dass in den letzten Beobachtungen seit 2010 ein Anstieg der Arbeitslosigkeit zu verzeichnen ist, der die in den vergangenen Jahrzehnten beobachtete Geschichte übertrifft.
Ein weiterer wichtiger Punkt, insbesondere im ökonometrischen Modellierungskontext, ist die Stationarität der Reihe; das heißt, sind Mittelwert und Varianz über die Zeit konstant?
Wenn diese Annahmen auf eine Variable nicht zutreffen, sprechen wir davon, dass die Reihe eine Einheitswurzel (nicht stationär) aufweist, was bedeutet, dass die Schocks, denen die Variable ausgesetzt ist, einen dauerhaften Effekt haben.
Dies scheint für die Variable, die Dauer der Arbeitslosigkeit, der Fall zu sein. Wir haben gesehen, dass die Schwankungen der Variablen sich erheblich verändert haben, was sich stark auf Wirtschaftstheorien auswirkt, die sich mit Zyklen befassen. Aber wie können wir, abgesehen von der Theorie, praktisch überprüfen, ob eine Variable stationär ist?
Das Prognosepaket bietet eine ausgezeichnete Funktion, die es ermöglicht, Tests wie ADF, KPSS und andere anzuwenden, die bereits die Anzahl der Differenzen zurückgeben, die erforderlich sind, damit die Reihe stationär ist:
#Verwendung des ADF-Tests zur Überprüfung der Stationarität forecast::ndiffs( x = econ$uempmed, test = "adf")

Hier zeigt der p-Wert, der größer als 0,05 ist, dass die Daten nicht stationär sind.
Ein weiterer wichtiger Punkt bei Zeitreihen ist die Identifizierung möglicher Korrelationen (der linearen Beziehung) zwischen den verzögerten Werten der Reihe. Die ACF- und PACF-Korrelationsdiagramme helfen bei der Identifizierung.
Da die Reihe keine Saisonalität, aber einen bestimmten Trend aufweist, sind die anfänglichen Autokorrelationen tendenziell groß und positiv, da zeitlich nahe Beobachtungen auch einen nahe beieinander liegenden Wert haben.
Daher neigt die Autokorrelationsfunktion (ACF) einer Trendzeitreihe dazu, positive Werte zu haben, die langsam abnehmen, wenn die Verzögerungen zunehmen.
#Residuen der Arbeitslosigkeit checkresiduals(econ$uempmed) pacf(econ$uempmed)
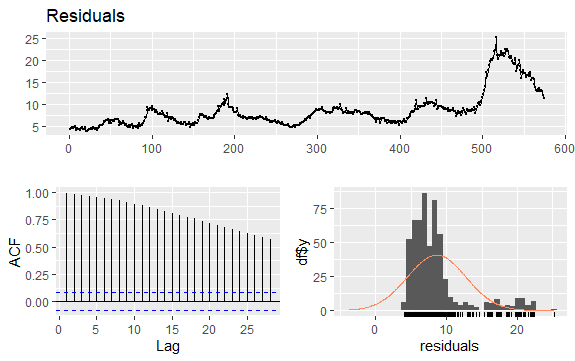
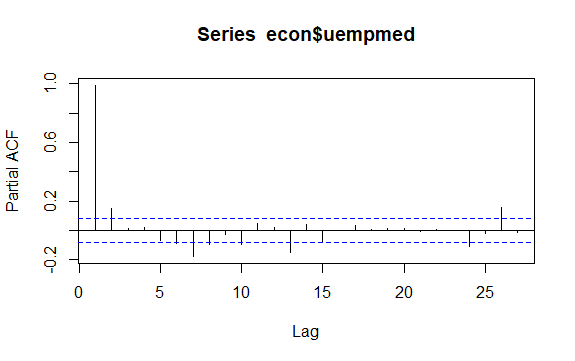
Fazit
Sobald wir mehr oder weniger saubere, d. h. bereits aufbereitete Daten vorliegen haben, sind wir oft geneigt, uns sofort in die Modellierungsphase zu stürzen, um erste Ergebnisse zu erzielen. Dieser Versuchung sollten Sie widerstehen und stattdessen mit der explorativen Datenanalyse beginnen, die uns auf einfache Weise dabei hilft, aussagekräftige Erkenntnisse aus den Daten zu gewinnen.
Sie können auch einige der besten Ressourcen zur Statistik für Data Science erkunden.